O aprendizado é feito por meio do ajuste dos pesos e da bias. O ajuste é feito, corrigindo os pesos, em etapas, a partir do erro calculado sobre o valor emitido pelo modelo, uma vez que a saída real já é conhecida, pois foi fornecida no conjunto de aprendizado. Isso é chamado de aprendizado supervisionado.
Após a rede emitir um resultado, podemos, então, calcular o erro. A forma mais simples, de se fazer isso, é subtraindo o valor predito, do esperado. No entanto, essa abordagem possui alguns problemas. O primeiro é que teremos erros positivos, e negativos. E ao somar esses erros, um pode anular, o outro. Por exemplo, se um erro é 1 e outro é menos 1, então, na média o erro é zero. Estamos interessados na magnitude do erro, e não se ele é positivo, ou negativo. Outro problema, com essa abordagem, é que queremos que os erros grandes sejam enfatizados, para que o modelo tente minimizá-los mais rapidamente. Nesse caso, a simples subtração não é apropriada. Uma abordagem, mais usada, é elevar a diferença ao quadrado. Agindo dessa forma, o erro será sempre positivo e os erros maiores serão mais destacados.
Na prática, o erro não é calculado para cada exemplo. O que é feito, é o cálculo da média dos erros, para todos os exemplos. Então, cada erro elevado ao quadrado é somado e, posteriormente, dividido pelo número de exemplos. Essa forma de cálculo de erro, é chamada de erro médio quadrático, ou MSE, do inglês, Mean squared Error. Funções que calculam o erro, são chamadas, de função de perda, ou loss function. A MSE, é uma função de perda, muito usada em regressão linear mas, para a regressão logística, ela não é apropriada. Isso ocorre porque, ao introduzimos a não linearidade da função logística, a superfície de erro em função dos pesos, se torna não convexa, e isso dificulta encontrar os valores de pesos, que tornam o erro mínimo. Explicaremos isso, com mais detalhes, mais adiante. No momento, é suficiente saber que precisamos de outra função de perda. No caso da regressão logística, a função mais adequada é a função de perda logística.
Para representar a função de perda, muitas vezes usamos a letra L, do inglês loss, tendo como argumento o valor predito, e o valor esperado. A função de perda logística, para o caso de classificação binária, é uma função, expressa na seguinte fórmula.
Esta formulação torna a
superfície de erro mais convexa, o que ajuda a achar quais valores de pesos gerariam o
menor erro. Note que, na fórmula,
o valor esperado, pode assumir o valor de 1, ou 0. Caso seja 1, a formula se resume ao formato
-log(ŷ). Indicando que,
quanto mais próximo de 1 for o valor previsto, menor será o erro. Caso seja 0, a formula se resume ao formato
-log(1-ŷ). Indicando que,
quanto mais próximo de 0 for o valor previsto, menor será o erro.
Como no caso da perda quadrática, o erro não é calculado para cada exemplo. O que é feito, é o cálculo da média dos erros para todos os exemplos. O erro médio é representado pela letra J, e possui como argumento, o vetor de pesos, e a bias. Ou seja, o erro depende apenas desses parâmetros.
Agora que já aprendemos a calcular o erro, o próximo passo, é ajustar os pesos e a bias, para minimizarmos esse erro. Mas como fazemos isso? A técnica mais usada, para fazer isso, é a técnica da descida do gradiente, ou, gradiente descendente. Vamos explicar agora, como é essa técnica.
Mas primeiro, vamos apresentar uma noção intuitiva da técnica. Se plotarmos um gráfico do erro em relação aos pesos, veremos que o erro forma uma superfície em um hiperplano. Se forem apenas dois pesos, fica mais fácil visualizar, pois o erro forma uma superfície em um espaço tridimensional. Na figura abaixo, temos os pesos, w1 e w2, e a altura é o erro J. O que queremos é chegar no ponto mais baixo dessa superfície, onde o erro é o menor possível.
Isso se parece, com a situação de um montanhista que quer descer de uma montanha.
Para isso, ele olha em volta, a partir do ponto, onde ele se encontra, e tenta ver, em qual direção, a inclinação para baixo é maior. Quando descobre essa direção, ele dá um passo nessa direção. Mas, enquanto vai descendo, ele está sempre olhando em volta, para ver se a inclinação mudou de direção, para que ele ajuste sua direção, para a maior inclinação. Essa inclinação, em uma superfície, em um espaço de várias dimensões, é chamada, na matemática, de gradiente. E como é calculada essa inclinação, ou gradiente? Vamos mostrar isso, o mais intuitivamente possível, usando o mínimo de ferramental matemático. Vamos mostrar, primeiramente, o cálculo da inclinação em uma função de uma variável, apesar de esse não ser o caso geral, da regressão logística, uma vez que o cálculo depende de vários parâmetros e pesos. No entanto, essa simplificação, nos ajuda a entender o cálculo da inclinação.
Vamos supor a função cujo o gráfico está ilustrado abaixo. Visualmente, podemos ver que o valor mínimo da função ocorre quando x está próximo ao valor 1.3. Isso pode ser calculado analiticamente, obtendo a função que expressa como varia a inclinação do gráfico da função. Isso, em matemática, é chamada de derivada da função. Os métodos, para obtenção de derivada de funções, é todo um capítulo na matemática, e foge do escopo deste post. No momento, basta sabermos que a derivada da função, é a mostrada, representada por um apóstrofo, no nome da função.
Em vermelho, podemos ver a curva da função derivada. Obtendo as raízes da função derivada (onde y é igual a 0), obtemos o valor de x, onde a inclinação é zero, ou seja, quando a curva inverte, e podemos descobrir o valor mais baixo da curva, caso exista. No entanto, quando se trabalha com dados experimentais, de várias dimensões, como no caso da regressão logística, não temos uma visão geral do comportamento da superfície de erro. É como o caso de um montanhista, tentando descer uma montanha no escuro. Ele só consegue saber a inclinação, na posição onde ele está. Nesse caso, não podemos descobrir os pontos mínimos da curva analiticamente. O que podemos fazer, é calcular a posição, em cada ponto, e mover na direção de maior inclinação.
Vamos exemplificar, essa procura pelo ponto de mínima, na forma não analítica, usando a equação mostrada. Suponha o valor de x igual a 0.8. Nesse ponto, se usarmos a função que expressa a inclinação, que é a derivada, o valor da inclinação é -3.75. Então, a inclinação é negativa, o que significa, que temos que andar no sentido contrário da inclinação, para descermos um pouco mais. Mas a pergunta é, qual é o tamanho desse passo? O tamanho desse passo, ou valor, é chamado de taxa de aprendizagem.
Na figura, podemos ver que, se essa taxa de aprendizagem for muito grande, o valor de x resultante vai ultrapassar o ponto de mínima. E se for muito pequeno, iremos precisar de muitos passos de cálculo para chegar ao ponto de mínima. Portanto, o valor da taxa de aprendizagem é muito importante para definirmos o modelo e muitas vezes, precisamos realizar vários testes para definirmos seu valor. Em outras palavras, seu valor é obtido de forma empírica. Valores, como a taxa de aprendizado, que são estabelecidos na criação do modelo, e não no ajuste do modelo, como é o caso dos pesos, são chamados de hiperparâmetros, para não confundir com os parâmetros, que são os pesos.
Vamos adotar, no nosso exemplo, o valor de 0.1, como taxa de aprendizagem. Nesse caso, o novo valor de x é 1.175, o que não ultrapassa o valor do mínimo, que é 1.3. Se tivéssemos adotado, o valor da taxa de aprendizagem, de 0.3, o novo valor de x seria 1.9, o que ultrapassa o valor do ponto mínimo da curva.
Vamos olhar um outro caso. Suponha que o valor de x seja -0.5. Nesse caso, o valor da derivada, nesse ponto é 2.5. Se caminharmos no sentido de descer a inclinação, usando a taxa de aprendizagem de 0.1, o próximo valor de x será de -0.75. Ou seja, vai caminhar no sentido contrário do menor mínimo, e vai se aproximar de uma inflexão na curva, que não é o ponto de menor mínimo. Esse mínimo que não é o menor da função é chamado de mínimo local, e o menor mínimo geral da função é chamado de mínimo global. Durante o ajuste do modelo, é possível que ele fique preso em um mínimo local e isso é um problema. Veremos, futuramente, técnicas que tentam evitar a ocorrência deste problema.
Mas, como falamos anteriormente, esse foi apenas um exemplo para entendermos como funciona o gradiente descendente. No caso da regressão logística, e de outros modelos de aprendizado de máquina, a função de erro depende de muitos parâmetros, formando um hiperplano em um espaço multidimensional, também chamado de espaço vetorial n-dimensional. Nesse caso, em cada direção, que nosso montanhista fictício olhar, existirá uma inclinação diferente. E é preciso calcular a inclinação em cada dimensão. Quando calculamos a inclinação, em um espaço vetorial de várias dimensões, o termo usado não é o termo derivada, e sim o termo gradiente. Daí o nome gradiente descendente. Precisamos calcular, a inclinação em cada dimensão, para sabermos onde a inclinação é maior. Na figura temos a inclinação, em cada dimensão, e a seta roxa indica, a direção da maior inclinação.
Agora que apresentamos a noção intuitiva, vamos apresentar a fórmula geral do gradiente para espaço vetorial, de n dimensões. A notação, para o gradiente de uma função, é a derivada parcial da função para cada uma das dimensões. A função tem como argumento, o vetor w, de pesos.
Portanto, para ajustar o peso a cada passo, devemos usar o valor do peso no passo anterior e subtrairmos o valor da taxa de aprendizagem multiplicada pela derivada da função de erro, em relação à dimensão representada pelo peso. Devemos subtrair pois estamos caminhando em sentido contrário da inclinação. O mesmo procedimento deve ser feito em relação à bias. Só falta, então, obtermos o valor da inclinação da função de erro em relação à cada dimensão. Como fazer para obter esse valor?
Abaixo temos o esquema completo, da regressão logística, e todas as fórmulas, envolvidas no processo. Podemos ver, que a função de erro, depende do valor predito, ŷ, emitido pela função sigmoide e esta, por sua vez, depende do valor de z, que é função do valor dos pesos e da bias. Então, precisamos obter a derivada, em relação a cada peso, e em relação à bias. Parece ser algo matematicamente complexo. No entanto, a derivada desta função complexa é simplesmente, o produto do valor da entrada pela diferença entre o valor predito e o valor esperado.
Sendo assim o ajuste dos pesos e da bias, a cada passo, é dado pelas duas fórmulas simples, mostradas abaixo. Então, agora temos a formulação completa, para realizar o aprendizado do modelo. Mas, antes de partirmos, para realizarmos sua implementação em Python, vamos apresentar mais alguns conceitos importantes.
O primeiro conceito, é o conceito de época. Uma época, é quando todos os exemplos foram passados, pelo modelo. O modelo, pode precisar passar por várias épocas, para que chegue a um erro mínimo, o que é chamado de convergência. No entanto, pode ocorrer, do modelo não convergir. O conjunto de exemplos, que é usado para ajustar o modelo, é chamado de conjunto de treinamento. Após ser ajustado, o modelo deve ser testado com outro conjunto de dados, chamado de conjunto de teste. Quando o modelo, tem um ótimo desempenho, no conjunto de treinamento, mas um desempenho ruim, no conjunto de teste, isso significa, que o modelo sofreu um sobre ajuste, ou overfitting. Ou seja, ele não foi capaz de gerar uma generalização, e ficou muito específico para o conjunto de treinamento. Isso deve ser evitado, e veremos formas de se fazer isso em outras aulas.Implementação
Vamos ver agora, como
implementar, a etapa de aprendizado. O código completo, está disponível, no
jupyter notebook. Abaixo, temos o código, em Python, para a preparação da execução. Nele temos, as
importações, dos módulos necessários, e a
inicialização das variáveis, que serão usadas. É importante lembrar, que este é um exemplo, sendo que os
dados são fictícios.
Vamos importar o módulo matplotlib.pyplot, para que possamos plotar, a evolução do erro médio. Também, iremos importar o módulo random, para gerarmos números pseudo aleatórios. Vamos importar, também, do módulo math, a função, exp, que ao receber um número, retorna o valor, do número de Euler, elevado a esse número. Usamos essa função, para criar, a nossa função sigmoide.
A entrada será definida por uma matriz de dez linhas por duas colunas, onde a coluna de índice 0, contém o valor do salário e a coluna de índice 1, contém o valor do pedido de empréstimo. As dez linhas representam dez casos de pedido de empréstimo. As saídas esperadas para treinar a rede é um vetor de 10 posições, onde o valor 0, indica que o pedido deve ser rejeitado, e 1, indica, que o pedido deve ser aceito. Vamos criar um vetor, de dez posições, para armazenar o valor dos erros de uma época. Em seguida, definimos aleatoriamente, o valor dos parâmetros, ou seja, dos pesos e da bias.
O próximo passo, é definirmos os valores dos hiper parâmetros, que neste caso, é o valor da taxa de aprendizagem, que vamos definir como um décimo, e o número de épocas, que vamos definir, com o valor de mil épocas. Vamos, também, definir um vetor, que vai armazenar o erro médio, de cada época, para podermos plotar a evolução do erro médio.
A próxima etapa, é a etapa de aprendizado. Nessa etapa é preciso percorrer todos os exemplos, em todas as épocas. Então, precisamos de dois laços, ou loops aninhados. Um para o números de épocas, e outro para os exemplos. A cada iteração, desses dois laços, iremos calcular o valor de z, para cada exemplo, usando o valor dos pesos atuais, e da bias. Depois iremos fazer a predição, usando a função sigmoide, e colocando o valor na variável ŷ. Após isso, calcularemos o erro corrente, e faremos o ajuste nos parâmetros, usando as fórmulas mencionadas anteriormente. Após passarmos por todos os exemplos, em uma época, calcularemos o erro médio da época, e armazenaremos o valor, no vetor de erros médios, para futura plotagem.
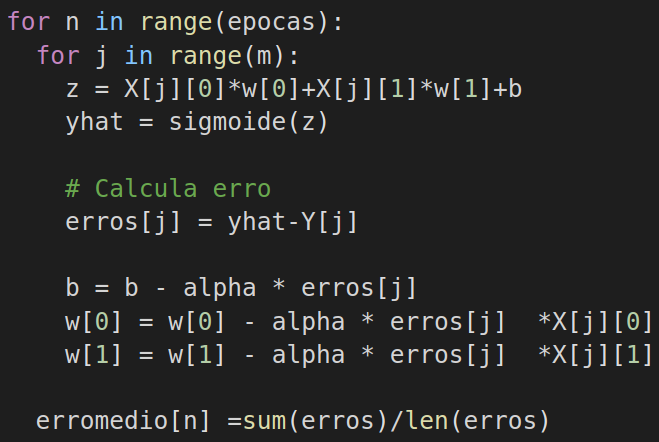
Em seguida, vem a etapa de verificação do aprendizado. O certo seria realizar isso, com outro conjunto de dados. O conjunto de testes. No entanto, esse é apenas um exemplo ilustrativo. Por isso, Iremos usar o mesmo conjunto de dados. O programa executa um loop, percorrendo cada pedido, e calculando z, e a predição. Também, plotamos a evolução do erro médio, armazenado na etapa anterior. O programa imprime, para cada pedido, os valores de entrada, e o que foi calculado.
No gráfico abaixo, que mostra a evolução do erro, ao longo das épocas, podemos ver que o erro varia muito nas primeiras épocas, e que, posteriormente, vai se estabilizando, e tendendo a zero.
Numpy
Por que Python, é uma das linguagens de programação mais populares, para quem trabalha com Inteligência artificial e aprendizado de máquina? De fato, Python é uma linguagem de alto nível, onde é possível realizar manipulações complexas, em estrutura de dados, com poucas linhas de código. Porém, a linguagem Python é substancialmente mais lenta na execução que outras linguagens, tais como a linguagem
C e
Julia. E, no caso de aprendizado de máquina, a velocidade de execução é fundamental. A resposta está, na
biblioteca de módulos do Python, principalmente, o módulo
Numpy.
Numpy significa Python Numérico e esse módulo é um projeto de código aberto, com o objetivo de habilitar a
computação numérica em Python. Também, possui funções, para trabalhar no domínio da álgebra linear, transformada de Fourier e matrizes. Numpy, utiliza códigos
C,
C++, e
Fortran, em Python. Essas linguagens de programação, rodam bem mais rápido, quando comparadas com Python. Um código que utiliza o módulo Numpy, pode executar até
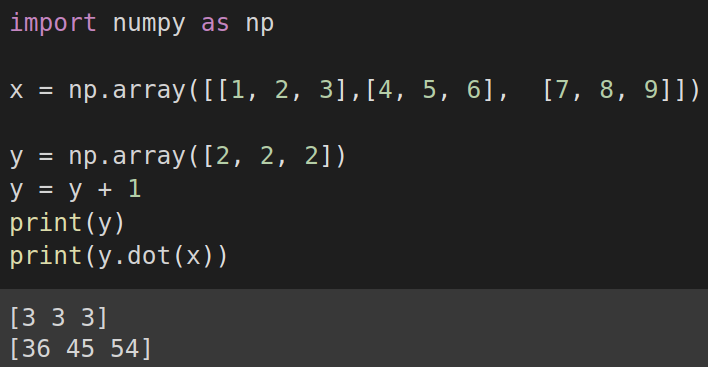
300 vezes mais rápido, do que um código que não usa o módulo. Vemos aqui, um exemplo de multiplicação, de uma matriz por um vetor. Com Numpy é possível realizar operações sobre vetores, e matrizes, com uma única chamada de função,
sem a necessidade do uso de laços de iterações.
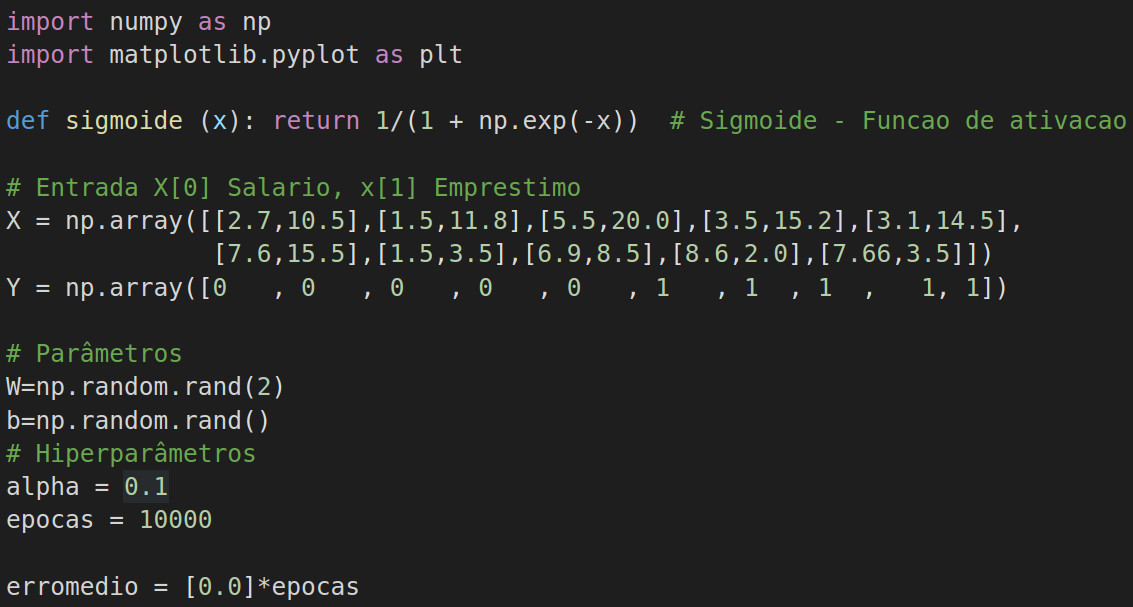
Vamos agora, alterar o código do nosso exemplo, para executar usando o módulo Numpy. Primeiramente, vamos importar o módulo Numpy. Vamos importar, o módulo matplotlib.pyplot, para que possamos plotar, a evolução do erro médio. Não é necessário importar, o módulo random, para gerarmos números, pseudo aleatórios, uma vez que o módulo Numpy, possui recursos para isso. Também, pela mesma razão, não é preciso importar o módulo math, para usar a função, exp. A função sigmoide, é definida usando a função exp do Numpy. Como anteriormente, a entrada será definida por uma matriz de dez linhas, por duas colunas, onde a coluna de índice 0, contém o valor do salário e a coluna de índice 1, contém o valor do pedido de empréstimo. As dez linhas, representam dez casos de pedido de empréstimo. Porém, a estrutura de dados não será uma matriz básica de Python, e sim, um array Numpy. Essa estrutura é implementada de forma, a poder ser operada, pela biblioteca Numpy, de forma eficiente. As saídas esperadas, para treinar a rede, também, são armazenadas, em um arrei Numpy. Em seguida, definimos aleatoriamente, o valor dos parâmetros, ou seja, dos pesos, e da bias, usando os recursos do Numpy. O argumento 2, para função rand, na definição dos pesos, indica que devem ser definidos, dois números aleatórios, que serão armazenados, em um array Numpy. O próximo passo é definirmos os valores dos hiperparâmetros, que neste caso, é o valor da taxa de aprendizagem, que vamos definir, como um décimo, e o número de épocas, que vamos definir com o valor de mil épocas. Vamos, também, definir um vetor, que vai armazenar o erro médio de cada época para podermos plotar a evolução do erro médio.
A próxima etapa, é a etapa de aprendizado. Nessa etapa, é preciso percorrer todos os exemplos, em todas as épocas.
No entanto, diferentemente da implementação anterior, no caso atual , não precisaremos de dois laços aninhados de execução. Isso porque, com o Numpy, é possível dispensar laços, para operar os elementos de um array Numpy, uma vez que ele realiza as operações em todos os elementos em um único comando e, se o hardware permitir, paralelamente. Então, precisaremos apenas do laço, para as épocas. A cada iteração desse laço, iremos calcular o valor de z, para cada exemplo, usando o valor dos pesos atuais, e da bias. Note que as variáveis armazenam estruturas em um array Numpy, e não valores simples. No cálculo de z é usada a função dot, do Numpy, que calcula o produto entre dois arrays. Depois, iremos fazer a predição, usando a função sigmoide, e colocando o valor, na variável ŷ. Novamente, destacamos que, a predição é feita para todos os exemplos, em uma única operação. Após isso, calcularemos o erro corrente, e faremos o ajuste nos parâmetros, usando as fórmulas mencionadas anteriormente. No ajuste dos pesos, podemos notar o operador T, aplicada antes, da função dot. O operador T, realiza a transposição do vetor, para possibilitar, a multiplicação entre os vetores. Nesse caso, entre o vetor de erro, e o vetor de entradas. Após passarmos por todos os exemplos, em uma época, calcularemos o erro médio da época, e armazenaremos o valor, no vetor de erros médios, para futura plotagem.

Ao, final, o programa imprime os valores dos pesos, e da bias ajustados, e plota o gráfico, com a evolução do erro.
No gráfico que mostra a evolução do erro ao longo das épocas. Podemos ver que o erro evolui de forma diferente nesta implementação, decaindo rapidamente para zero.
Só mais uma informação, antes de terminarmos. Existem módulos
Python, que implementam, a regressão logística, e outros modelos de aprendizado de máquina, sem que o programador precise realizar a implementação. Um desses módulos é o
scikit-learn. Veremos o uso desse módulo nos próximos posts.
Para quem desejar ver o
vídeo desta aula, ela está disponível em nosso canal. Nosso
curso completo de redes neurais está disponível neste
link.














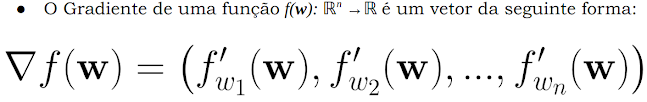










Comentários
Postar um comentário